이번 글은 플랜트 설계시에 작동유체가 흐를 때 발생되는 배관, Valve 및 Fitting 에서의 압력강하 (Pressure Drop)에 대한 첫번째 이야기입니다.
플랜트 설계 업무 중 유체 흐름에 대한 이해와 배관, GTG, STG, HRSG, 펌프 등의 Design Condition을 결정하기 위한 배관, Valve 및 Fitting 의 압력 손실 (마찰손실) 산출시에 아주 유용한 참고 자료가 되었으면 합니다.
Pressure Drop Calculation (Pipings, Valves and Fittings, Part I )
1. Introduction
플랜트의 배관 시스템을 설계하려면 우선 유체 역학에 대한 지식,이해 및 공학적 감각이 필요하다. 플랜트에 설치되는 배관, Valve 및 Fitting 류의 압력강하 (Pressure Drop)를 산출하는 방식에는 크게 등가길이법(Equivalent Length Method), K-팩터법 (K-factor Method) 등이 있다.
이 방법들 사이의 중요한 차이는 배관의 마찰 계수와 밸브 및 피팅류에 대한 등가 길이 "L/D" 및 저항 계수 "K" 사이의 저항 값의 개념이다.
실업무에서는 등가 길이 "L/D" 대신 마찰 손실 계수 "K" 를 적용한 배관, Valve 및 Fitting 의 저항 (또는 마찰) 손실 계산치는 실제 실험을 통해 입증한 값과 큰 오차가 없는 것으로 알려져 있으며, 따라서 이 글에서는 이 방법을 기준으로 배관, Valves 및 Fittings 류의 압력 손실(Pressure Drop) 계산 방법에 대해서 설명하고자 한다.
2. 유체의 물리적 특성 ( Physical Properties of The Fluid )
점도 (Viscosity) :
점도는 유체가 외력에 의해 작용할 때 흐르는 준비 상태를 나타내며, 즉 유체의 흐름의 어려움의 크기를 나타내는 양(끈적거림의 정도)으로 유체의 절대 점도는 내부 변형 또는 전단에 대한 저항의 척도이다. 다시말해서 점도란 유동성을 나타내는 중요한 성질로 유체를 이동시키려할 때 나타나는 내부저항을 말하며 역학점도(dynamic viscosity) 또는 절대점도(absolute viscosity)라고도 부른다.
물은 비교적 점성 작은편에 속하며 기체의 점도는 물에 비해 매우 작다.
20℃ 온도에서 물의 점도는 거의 1 cP 또는 0.001 Pas 이다. 대부분 유체의 점도는 예측할 수 있지만 일부의 경우 점도는 유체의 이전 작업에 따라 달라진다, 예를들면 프린터 잉크, 목재 펄프 슬러리 및 케첩은 점도의 요변성 특성을 갖는 유체에 해당한다.
실업무를 수행할 때 점도 단위와 관련하여 상당한 많이 혼동스러웠던 경험이 있었을 거라고 판단된다. 따라서 공식에 점도 값을 대입할 때마다 적절한 단위가 사용되도록 해야 한다.
| 절대점도 ( Absolute Viscosity or Dynamic Viscosity ) μ : in cP unit μ’ : in Pa s unit |
절대 점도는 프랑스의 Poiseille 라는 물리학자가 최초로 정의한 개념으로 그의 이름에서 따온 “Poise( P )” 라는 단위를 사용한다. 절대점도는 유체 그자체의 고유한 점성저항력을 나타냄 |
[ CGS 단위 ] 1 P = 1 g/cm s 1 P= 1 g/cm s = 100 cP ( cP =CetiPoise) [ SI 단위 ] 1 Pa s = 1 N s/ m2 = 1kg/m s 1 Pa s = 10 P (poise) 1 Pa s = 1000 cP (CentiPoise) 1 cP = 10-3 Pa s |
| 동점도 (Kinematic Viscosity) |
동점도는 점도를 그유체의 밀도로 나눈 점도로 점성저항력 을 나타내며 동점도는 배관(pipe line)내부에 흐르는 유체의 흐름에 매우 중요한 지표가 된다. 동점도는 St로 표시하고 단위는 ㎠/s 이며 1/100 로 줄여서 cS t를 사용한다. |
1 cSt = 0.01 St = 0.000001 m2/s = 1 mm2/s |
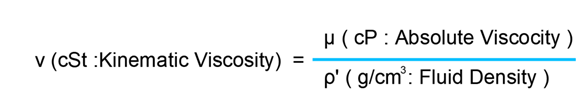 |
||
온도가 상승하면 액체의 점도가 감소하는 반면 기체의 점도는 증가하며, 액체 및 완전 기체의 점도에 대한 압력의 영향은 너무 작아서 대부분의 흐름 문제에서 실질적으로 무시되어 진다. 그러나 포화 또는 약간 과열된 증기의 점도는 증기 압력 변화에 따라 많이 변화된다는 것을 인식해야 한다. 특히 스팀이 아닌 Vapour 의 경우는 적절하게 적용해야 할 데이터가 없기 때문에 압력의 영향을 무시하여도 된다,
밀도, 비중: 물질의 밀도는 단위 부피당 질량입니다. 일관된 SI 밀도 단위는 입방 미터당 킬로그램(kg/m3)이며 이 글에서 기호 지정은 ρ(kg/m3 / ρ’ : (g/cm3), 1 g/cm3 or 1 g/ml = 1000 kg/m3 ) 이다. 또한, 비체적 (υ : Specific Volume) 은 밀도의 역수로 SI 단위는 킬로그램당 세제곱미터 (m3/kg, 1 litre/kg or 1 dm3/kg = 0.001 m3/kg )이다.

일반적으로 매우 높은 압력에서 액체의 밀도에 대한 압력의 영향은 흐름 문제에서 실질적으로 중요하지 않지만, 가스와 증기의 밀도는 압력 변화에 따라 크게 변화된다. 소위 기체의 경우, 밀도는 이상기체 방정식을 사용하여 밀도가 계산될 수 있다




액체(Liquid)의 비중(또는 상대 밀도)은 밀도의 상대적인 척도로서, 압력은 액체의 밀도에 큰 영향을 미치지 않기 때문에 온도가 비중의 기준을 정할 때 고려해야 할 유일한 조건입니다. 액체의 비중은 특정 온도에서의 밀도와 일부 표준 온도에서의 물의 밀도 비율입니다. 일반적으로 온도는 동일하며 15.6 ℃ ( 60 ℉)가 일반적으로 사용된다.

기체의 비중은 기체의 비율로 정의되며, 기체의 분자량과 공기의 분자량, 그리고 공기의 개별 기체 상수와 기체의 개별 기체 상수의 비율로 표시된다. 따라서 가스비중의 기준이 되는 물질은 공기이며, 가스의 무게와 공기의 무게를 비교한 값이 비중이 된다. 기체의 질량과 그 기체와 같은 조건 체적의 공기 질량과의 무게비를 뜻하며, 일반적으로 표준상태(0 ℃, 1atm)의 기체와 표준상태의 공기를 비교한다. 이때 공기의 기준 부피( 22.4 ℓ, 1mol )의 질량은 29g이다.

예를 들어 CH4 ( M= 12+4 =16 g) 의 비중을 구할경우 0.55 가 된다.

3. 유체 흐름의 특성 ( Nature of Fluid Flow )
유체 흐름의 한 가지 특성은 속도이며, 속도의 크기에 따라 세 가지 고유한 흐름 체계로 분류할 수 있습니다. 이 세가지 유형의 흐름은 ;
층류 (Laminar Flow) : Re (Reynolds No) < 2,100
서로 유체끼리 잘 붙어 있기 때문에 흐를때에 층을 이루며 흐르는 유동, 즉 입자가 서로 잘 붙어있기 때문에 확산이 잘되지 않으며, 진행방향으로 층을 이루며 거동한다. 층류에서는 중심 유속이 평균 유속의 2 배 정도가 된다.
천이 구역 (구간) ( Transition Zone) : 2,100 ≤ Re (Reynold No.) ≤ 4,000
층류에서 난류로 변화하는 사이의 어떤 구간으로, 천이가 시작되는 Reynold No. 를 임계 Reynolds no 라고 한다. 이 구간은 유체가 갖고 있는 관성력이 유체의 점성력을 벗어나기 시작하는 것으로 볼수 있다.
난류 (Turbulent Flow) : 유체 유동 중에서 무질서하고 비정상성을 가지는 유동으로 매우 불규칙하여 배관 내 흐름이 난류가 되면 유체의 마찰저항이 급격히 증가한다.
아래 그림은 그림 3-1은 염료가 주입된 흐름의 세 가지 가능한 유형을 보여줍니다.
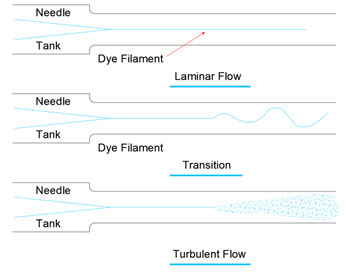
*** 실제적으로는 Re 2,000 – 3,000 사이의 유동 특성은 정확하게 정의하기가 어려움.
*** Reynolds no 로 층류, 난류를 판단하는 것은 원형관, 평판등에 따라 다르고 실험조건에 따라 다를수 있다.
4. 에너지 방정식 ( ENERGY EQUATION FOR FLUID FLOW )
4.1 베르누이 방정식 ( Bernoulli’s Theorem )
Bernoulli 정리는 도관의 유체 흐름에 대한 에너지 보존 법칙의 적용을 표현하는 방범으로, 임의의 수평 기준면 위의 특정 지점에서의 총 에너지는 다음과 같이 위치수두, 압력 수두 및 속도 수두의 합과 같다.

마찰 손실이 무시되고 배관 시스템(즉, 펌프 또는 터빈)에 에너지가 추가되거나 공급되지 않는 경우, 아래 방정식의 총 수두(H)는 유체의 모든 지점에 대해 상수가 된다.

그러나 실제 유동에서는 손실이나 에너지 증가 또는 감소가 발생하므로 이런 조건이 베르누이 방정식에 고려되어야 한다. 따라서 위의 그림에서 작동 유체의 두 점에 대해 에너지 균형 방정식을 작성할 수 있으며, 포인트 1 지점에서 포인트 2 지점까지의 파이프 마찰 손실 (hL : 헤드 손실) 을 반영하면 위에 방정식은 다음과 같이 된다.
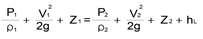
4.2 압력 측정
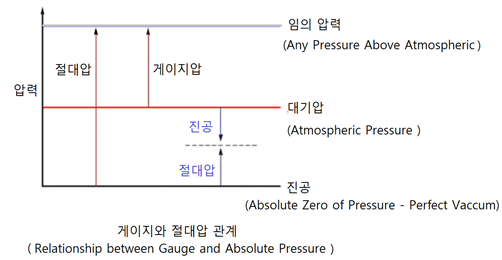
아래 그림은 게이지 압력과 절대 압력 사이의 관계를 그래픽으로 보여주며, 완전 진공은 지구 표면에 존재할 수 없지만 그럼에도 불구하고 압력 측정을 위한 편리한 기준이 된다
"표준" 기압은 1.0332 Kg/cm2(14.6959 lbf/in2) 또는 수은 760 mmHg 이며, 게이지 압력은 대기압 이상에서 측정되는 반면 절대 압력 (대기압+게이지압)은 항상 완벽한 진공 상태를 기준으로 한다.
진공은 대기 수준 이하의 압력 강하로 진공 상태에 대한 언급은 종종 수은 기둥 또는 물 기둥의 높이로 절대 압력을 표현한다.
5. 배관 시스템에 사용되는 밸브 및 피팅의 유형 (Types of Valves and Fittings used in Pipe Systems)
1) 밸브:
플랜트에는 사용되는 밸브는 매우 다양한 방법으로 설계되기 때문에 실질적으로 철저한 분류가 불가능하다. 밸브를 분류한다면, 밸브에 유체가 흐를 때 발생되는 저항에 따라 게이트 (Gate), 볼(Ball) , 플러그(Plug) 및 버터플라이 밸브(Butterfly)등과 같이 직통 유로를 나타내는 밸브는 낮은 저항 등급에 속하고 유로 방향이 변경되는 밸브는 글로브 및 앵글 밸브와 같은 것은 높은 저항 등급에 속한다.

2) 배관 부속 자재 (Fittings):
피팅은 작동 유체의 분기(Branching), 축소(Reducing), 확장(Expending) 또는 편향(Deflecting)을 위해 사용되는 용도에 따라 분류할 수 있으며, 티 (Tee), 크로스(Cross), 측면 출구 엘보우(Elbow) 등과 같은 피팅은 분기 피팅이라고 할 수 있다.
피팅을 줄이거나 확장하는 것은 유체 통로의 면적을 변경하는 것으로, 이러한 피팅에는 Reducer 및 부싱, 편향 피팅, Bend, Elbow, Return Bend 등이 있으며 이것. 흐름양과 방향을 바꾸는 것들이다.
물론 일부 부속자재는 일반적인 분류의 조합일 수 있으며, , 커플링 및 유니언과 같은 유형은 흐름에 대한 현저한 저항을 제공하지 않으므로 여기서 배관 설치시 압력 강하에 대한 고려할 필요 없다.

To be continued in the next article.